Alicia Boole (1860-1940): The Woman from Cork who ‘Saw the Fourth Dimension’

Written by Dr. Andrew Flynn, School of Mathematical Sciences

There is no doubt that ‘Boole’ is in the air when walking through UCC’s main campus. The Boole Library, Boole Lecture Theatres, the impressive bronze bust looking on as the crowds pass – everyone who passes through UCC is aware of George Boole, or perhaps even studied Boolean algebra, the mathematics he developed which became the cradle of the Digital Age. However, it may surprise you that another Boole, born in Cork 165 years ago, developed one of the methods we use today to visualise objects from the fourth dimension. George and Mary Boole’s daughter, Alicia, was an incredibly gifted mathematician, and though her story is known by few, she has entered the annals of mathematics as ‘the woman who saw the fourth dimension’.

Alicia Boole, born on the 8th of June 1860

Alicia Boole, born on the 8th of June 1860, was the third of George and Mary’s five daughters. Her father was the first Professor of Mathematics in UCC, whose work laid the foundations of modern computing; her mother was a forward-thinking educationalist with a deep interest in mathematics. Sadly, Alicia’s early life was marred by tragedy. Her father passed away when she was just four years old, leaving her mother to care for five children in challenging circumstances. It was not long after George’s death that Mary left for London with Alicia’s sisters, while Alicia remained in Cork living under the care of her grandmother and great-uncle: John Ryall, UCC’s first Vice-President (1845–75) and Professor of Greek. What followed were difficult years for the Boole family, and Alicia was eleven when she was finally reunited with her mother and sisters.

Alicia was introduced to the world of higher-dimensional geometry

During her teenage years, Alicia was introduced to the world of higher-dimensional geometry by the mathematician Charles Howard Hinton, who later married Alicia’s sister. The name Hinton may ring a bell, as Charles is the great-grandfather of the 2024 Nobel Prize in Physics winner, Geoffrey Hinton, known to many as the ‘Godfather of AI’. During one of their early meetings, Charles presented Alicia with a set of small wooden cubes, which she experimented with extensively, using them to peer into the fourth dimension, and subsequently developed a method that enabled her to visualise objects from the fourth dimension.

Imagining the fourth dimension is like trying to imagine what a three-dimensional object looks like based on its shadow. While we live in a three-dimensional world, mathematics enables us to see into as many dimensions as we like, and Alicia’s method allows us to do just that. Her method is based on ‘unfolding’ four-dimensional objects to visualise them in three-dimensional space. She introduced the word ‘polytope’ into the English language to describe the four-dimensional versions of polyhedra and polygons, i.e. four-dimensional versions of cubes and squares, pyramids and triangles, etc. The most famous of these polytopes is the four-dimensional cube, commonly known as ‘the tesseract’, a term coined by Alicia’s brother-in-law Charles.

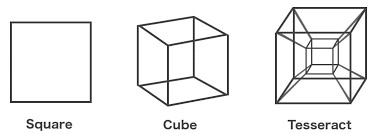
Alicia painstakingly built cardboard cross-sections of polytopes

Unlike many mathematicians of her time, who approached geometry analytically (through pen and paper), Alicia painstakingly built cardboard cross-sections of polytopes, effectively ‘seeing’ the fourth dimension in a way that few others could. Using her method, Alicia went on to discover that there exists a family of six regular convex polytopes in the fourth-dimension, meaning that these polytopes have certain mathematical properties: the line of the shortest distance between two points on the surface of an object is always contained within the object. Alicia was unaware that, before she was born, the same six polytopes had been discovered analytically by the Swiss mathematician Ludwig Schlaefli. Alicia constructed her models purely from curiosity, her ability to understand and transport these higher-dimensional objects to our world without any formal training was extraordinary, yet her work went largely unnoticed.

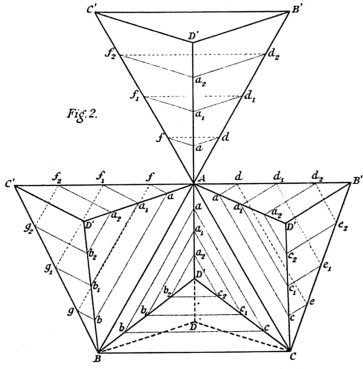
Part of an unfolded hyperoctahedron. From Alicia Boole Stott: On Certain Series of Sections of the Regular Four dimensional Hypersolids (Amsterdam: Johannes Müller,1900). Boole Papers, Special Collections, UCC Library.

At the age of 30

At the age of 30, Alicia married Walter Stott, an actuary, and soon devoted herself to raising their two children, Mary and Leonard. However, her passion for four-dimensional geometry never truly faded. It was Alicia’s husband who later reawakened her interest in mathematics by bringing her attention to the work of the Dutch mathematician Pieter Hendrik Schoute. After recognising the similarities between their research interests, Alicia reached out and sent pictures of her models to Schoute. Impressed by her work, Schoute immediately travelled to London to meet Alicia and invite her to collaborate, marking the beginning of a highly productive partnership. In the 20 plus years that followed, they co-authored several papers that significantly advanced our understanding of polytopes. Among their most notable works were ‘On Certain Series of Sections of the Regular Four-Dimensional Hypersolids’ (1900) and ‘Geometrical Deduction of Semiregular from Regular Polytopes and Space Fillings’ (1910). Schoute, who had a more analytical approach, benefited immensely from Alicia’s incredible visualisation skills.

3-D Prints of a range of sections of the polytopes – front and centre is a solid 120 cell, behind it two smaller versions of the same section with the ‘skin’ removed, so that internal forms can be seen; around them are 5-cell, 8-cell, 16-cell and 24-cell sections. Printing courtesy of the Digital Scholarship Studio, Boole Library. Image: Fergal Gaynor & Andrew Flynn.

At the age of 54

In 1914, at the age of 54, Alicia finally received formal acknowledgment of her contributions when the University of Groningen awarded her an honorary doctorate and held an exhibition of her models. These models are part of the University Museum’s collection in Groningen.

Models of polytope sections by Alicia Stott Boole, on display in the University Museum Groningen. Photo Erik Jaap Dijk. Image reproduced by kind permission of University Museum Groningen.

Alicia’s story mirrors that of many women in science

Though her work was groundbreaking, Alicia’s story mirrors that of many women in science; brilliant, but largely unnoticed. The lack of awareness surrounding her achievements is particularly striking when considering that her father’s life and work are so widely celebrated. However, using today’s terminology, Alicia was by no means a ‘nepo baby’. Despite being the daughter of a renowned mathematician, Alicia did not benefit from his fame in any tangible way, her achievements are truly her own and were shaped by self-driven curiosity.

The rediscovery of her work decades after her death in 1940 has led to a renewed appreciation of her role in the history of mathematics. In 2001, a collection of her visually-striking coloured drawings of polytopes was found at the University of Groningen. These drawings, which had been largely forgotten, showcased her extraordinary ability to visualise and construct complex objects beyond our three-dimensional world.

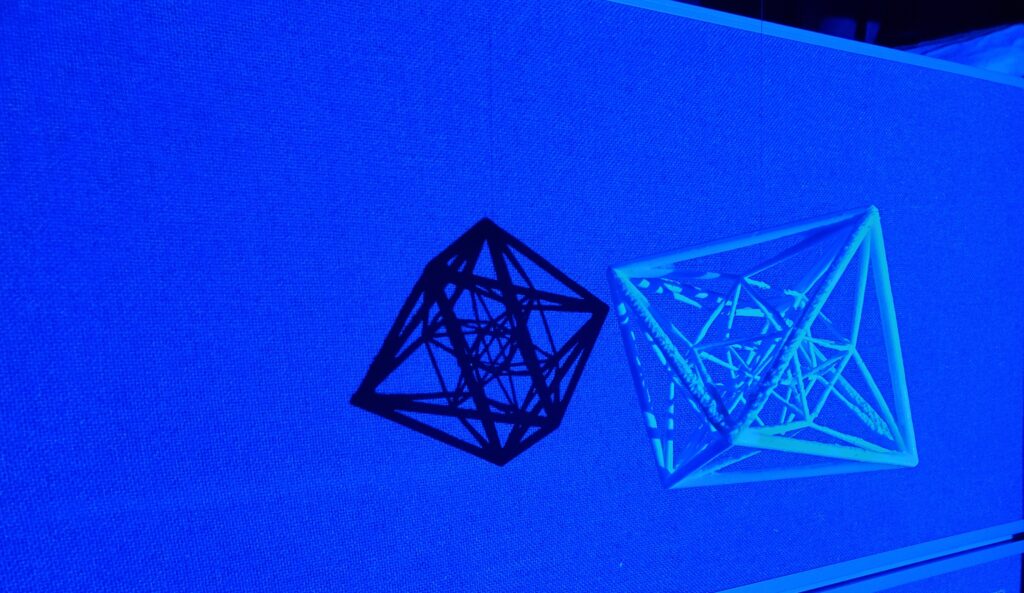
Section of a 24-cell polytope and its shadow. 3D printing courtesy of the Digital Scholarship Studio, Boole Library. Image: Fergal Gaynor & Andrew Flynn.

Her work laid the foundation for future explorations

While Alicia never held a formal academic position, her work laid the foundation for future explorations in higher-dimensional geometry. Her inspiring story is not just one of mathematical brilliance, but also of perseverance in the face of societal limitations. As we continue to uncover and celebrate these ‘hidden figures’, we must also ensure that future generations of women in mathematics and science receive the recognition they deserve, not decades after their contributions, but during their lifetimes.

Alicia was, in every sense, the woman who saw the fourth dimension, and it is time the world saw her.

Sections of a 120-cell polytope. 3D printing courtesy of the Digital Scholarship Studio, Boole Library. Image: Fergal Gaynor & Andrew Flynn.

Addendum

Fergal Gaynor

This year for the International Day of Mathematics on March 14th (3.14, i.e. Pi, get it?), and in honour of the remarkable Alicia Boole Stott, the UCC Boole Library’s Digital Scholarship Studio have teamed up with Dr. Andrew Flynn from UCC’s School of Mathematical Sciences to 3D print members of her family of polytopes. We have interspersed this article by Dr. Flynn with images of the results, cross-sections of a mathematical reality with an added dimension.

Some of the images show the object casting their two-dimensional shadow. These are inspired by the work of Marcel Duchamp, one of the 20th Century’s most influential artists. He conceived of his ‘ready-mades’, simple objects like a snow shovel (In Advance of a Broken Arm [1915]), picked from ordinary life and appointed to the status of art by the artist, as three-dimensional shadows cast by objects (hyper-objects) existing in the fourth dimension (he had been reading popular accounts of the work of mathematician Henri Poincaré). Some curators exhibit the ready-mades with this in mind, suspending them in space in a set-aside part of the gallery, illuminated in such a way as to ensure that the viewer sees them accompanied by their shadow. And accompanied also, perhaps, by the invisible affair of which the snow shovel is itself the shadow . . .

Section of a 16-cell polytope and its shadow. 3D printing courtesy of the Digital Scholarship Studio, Boole Library. Image: Fergal Gaynor & Andrew Flynn.